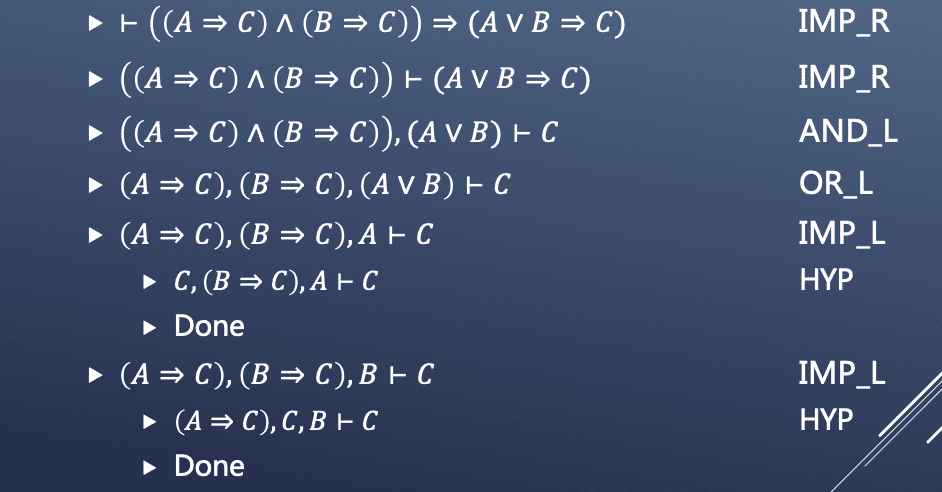这一系列(共 4 部分)为整理后的形式化语言与自动机的本科课程笔记,可作为知识提纲。
目录
I:概念,推理与文法
核心问题:哪些问题可以通过计算解决(可计算型理论)
自动机理论:研究抽象机器所能解决问题的理论(图灵机:核心理论模型;以及有限状态机、文法、下推自动机等)
谓词逻辑与集合关系
-
n 元关系是定义在某域上的一组 n 元组的集合
-
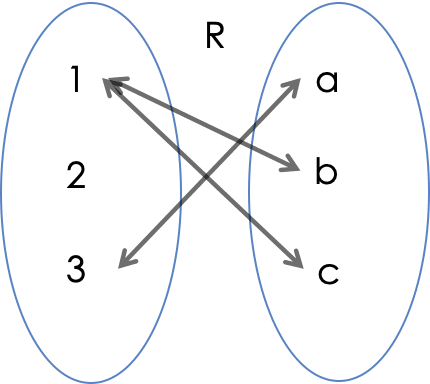
集合 A 和 B 的二元关系 R 是 A×B 的子集;二元关系可写作 xRy
-
dom (R) 和 ran (R) 分别表示关系 R 的定义域和值域
- 对于 几种特殊的关系:
- 偏序关系:自反,反对称,传递 Eg. 自然数集合 N 和小于等于关系≤构成的偏序集
- 等价关系:自反,对称,传递 -> 等价类:由等价关系确定的一组集合,每个集合中的任意元素都相互等价
- 等价关系的秩:等价类的个数
字母表、图与语言
- 字母表是语言中出现的原子符号,通常用 Σ 表示
- 字符串是字母表中元素的序列,长度必须为有限的,长度、连接等操作在定义上都为递归
- 长度:递归定义
- 字符串运算:联结运算 abc.def、重复运算 (abc)*
- 和集合有关的运算:
- 若 为字母表,则 为长度为 n 的字符串集合
- 正闭包、克林闭包
- 和集合有关的运算:
- 语言:一系列特殊字符串的集合:L⊆Σ^∗
- 图:系统描述方式
- 标签集合 D,标签函数 L:S∪T→D
- 带标签的图可以表示为一个 4 元组 (S,T,D,L)
- 树是一种特殊的有向无环图
- 迁移系统:
- 给定字符串是否属于某个具体语言 L? 任何问题都可以转换成语言问题
- (可判定问题与不可判定问题)
逻辑语言与演绎推理
-
证明:演绎法、归纳法与反证法
-
命题逻辑
- 一种可以判定真或假的命题描述语言
- 由原子命题和连接算子构成
-
谓词逻辑:比命题逻辑描述能力更强的逻辑语言,增加了变量取值
- 组成:Variable, Functions & (Predicate symbols, equality, logical connectives, quantifiers)
- 公式 在一个给定的结构 M 和赋值 下成立,记为 或
- 在给定结构 M 下每个赋值成立,记为或
- 任意赋值成立:
-
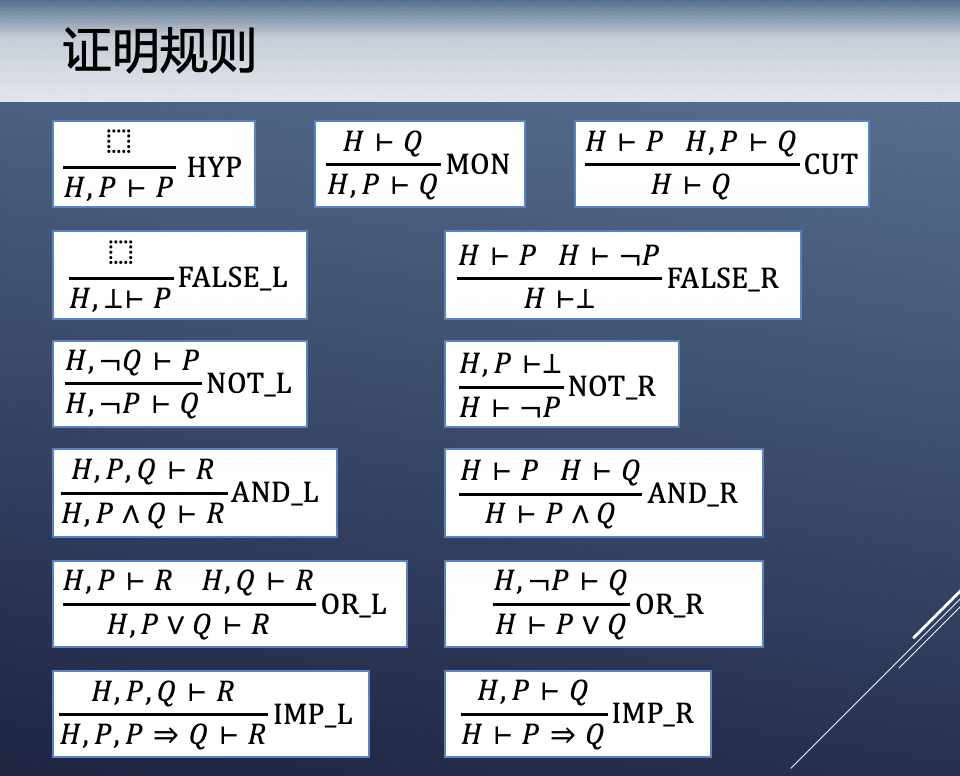
演绎推理
文法
概念
-
包含: V (ariables) T (erminal symbols) P (roductions /rules) S (tart symbols)
- V: 非终止符号,满足
- S: 起始符号,满足
-
文法的推导:Let G=(V,T,P,S)$$,. 有, 则称
- 上述过程 = 规约成
- 最左 & 最右,依据替换次序的不同,一个语句可以有多种推导
-
文法的语言:
-
符号上的描述: + 和 * 作为幂时表示长度为 1 以上 或 0 以上的表达式,如 等
-
定义:等价文法:如果 ,则等价
文法分类的乔姆斯基体系
0 型文法
由文法结构定义的文法,又称为递归可枚举文法、短语结构语言、递归可枚举集等
Phrase structure grammer, aka PSG
1 型文法
满足:
又称上下文有关文法 Context sensitive grammar aka CSG
2 型文法
满足: 且
又称上下文无关文法 Context free grammar, aka CFG
例如:T = {a, b},
3 型文法
满足: 具备形式:
或 ,其中
又称正则文法 / 正规文法 Regular grammar, aka RG
定义上讲,空语句 在 1 - 3 型文法中都是不允许的,但因为其不影响语言的有穷描述的存在,所以允许 存在,但其除了用于产生空语句以外不可用于其他任何句子的推导之中。
II: 有穷自动机与正则语言
有穷自动机 Finite Automation
动机:语言的识别:
- 为了证明 ,需推导 G,或规约 w,缺乏目的性和方向性
- 设计一套系统,提高识别效率,简介抽象、直观描述
定义
五元组:
-
Q 非空集合; 输入字母表, 状态转移函数, 开始状态, 终止 / 接收状态
-
表示在 q 状态下读入 a 转移到 p。
FA 的表达方式:函数或转换表(更直观)
字符串集合:
Instant Description 瞬时描述
表示自动机识别一个输入串的过程。形式:,x 为已处理的字符,y 为未处理的字符
有:,,其中 与文法中的转换 有类似的表达方式(+: 至少一次,*: 若干次,n: n 次 等)
- 如 表示 M 经过 n 次移动。从状态 转换成了状态 。
确定有穷状态自动机 Deterministic Finite Automaton, DFA
对于任意
关于 与 :前者为后者的扩充,有,用于识别语言
注意到后者定义域 为前者定义域 的真子集,所以二者如果有相同的值,不用区别符号,故常用 代替 。
非确定有穷状态自动机 Nondeterministic Finite Automaton, NFA
定义类似 DFA 的五元组:
其中 允许选择多个状态。即
FA 的 ID 与描述方式对 DFA 同样有效
空迁移
定义五元组:
在 NFA 的基础上,进一步允许 满足:。
即允许 M 在状态 q 下不输入任何字符而选择改变状态,做空移动,称为 。
空迁移 NFA 同样和 NFA 具有等价性。
注意在 -NFA 中, 与 不等价,需要根据上下文区分。
正则语言 / 表达式
正则表达式 Regular Expression - 使用适当的约定用更简洁的方式来表达文法 FA 所表达的语言
FA 是正则语言的识别器(有限自动机和正则表达式等价)
定义: 是正则表达式,表示语言
若 是正则表达式,表示语言 {a};
若 r 和 s 是 RE,则 是正则表达式, 是正则表达式。
- 正则语言 L (RE):有
⭐️ 正则语言的证明:泵引理 Pumping Lemma
- 泵引理:L 为一个正则语言,则存在一个常数 N,使得 若 ,能把 z 分为三个部分 xyz 满足有:。
利用反证法可以证明 L 不为正则语言。(找到恰当的拆分,并得到一个反例即可)
泵引理只是一个 RG 的必要条件,不可用于证明一个而语言是 RG。
Myhill-Nerode Theorem 迈希尔尼罗德定理:L 是正则语言,当且仅当 RL 有有限的等价类。
是一个证明语言是正则语言的必要充分条件。
正则语言的封闭性
- RL 对于并、乘积、闭包运算封闭
- RL 对于补、交运算封闭
自动机的转换
通常的转换顺序: RE -> -NFA -> NFA -> DFA
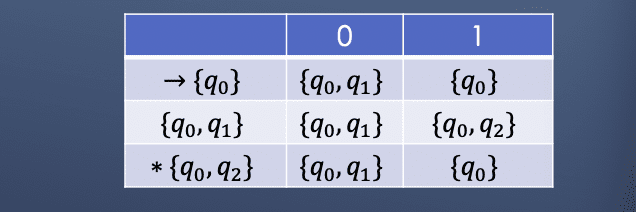
NFA -> DFA 及等价性
如果能用 NFA 来表示的语言,同样可以使用 DFA 来表示:

接下来移除不可到达的状态集合得到:
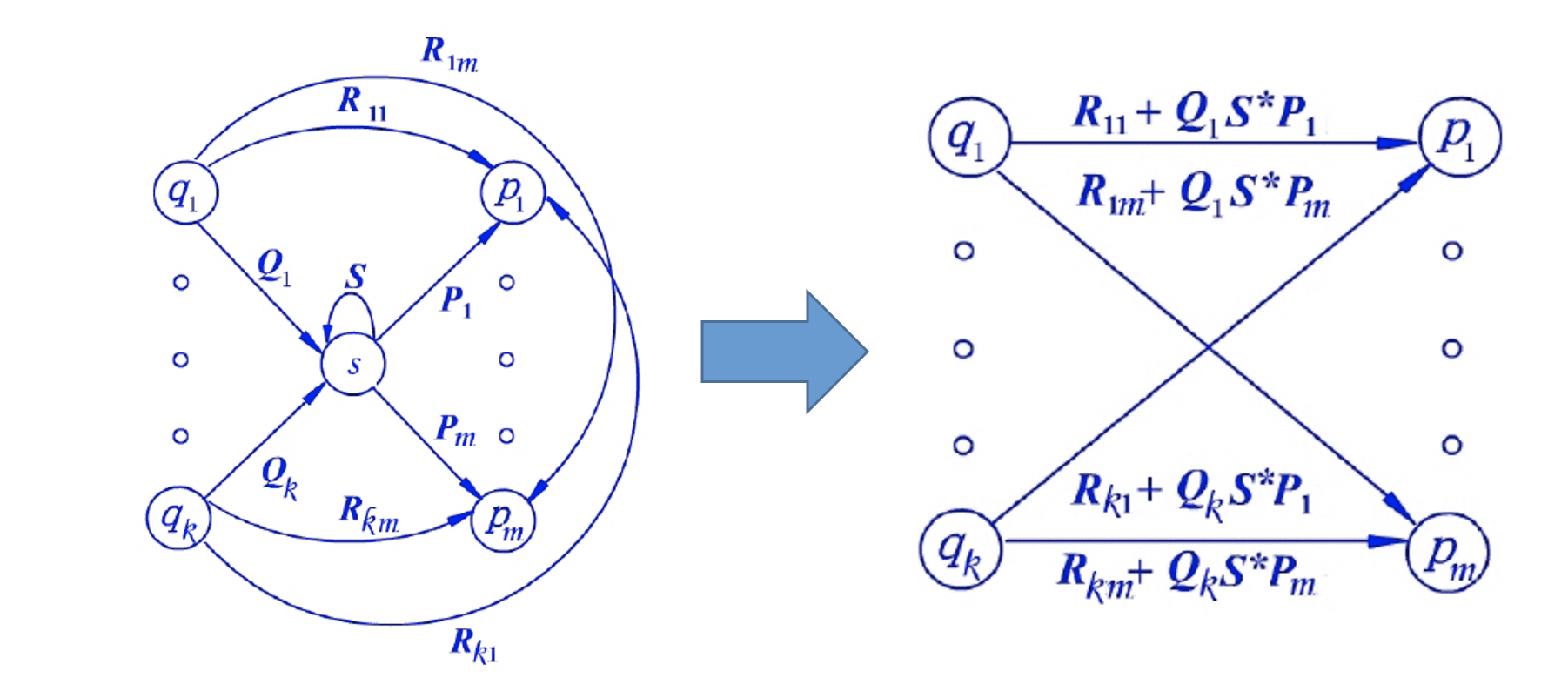
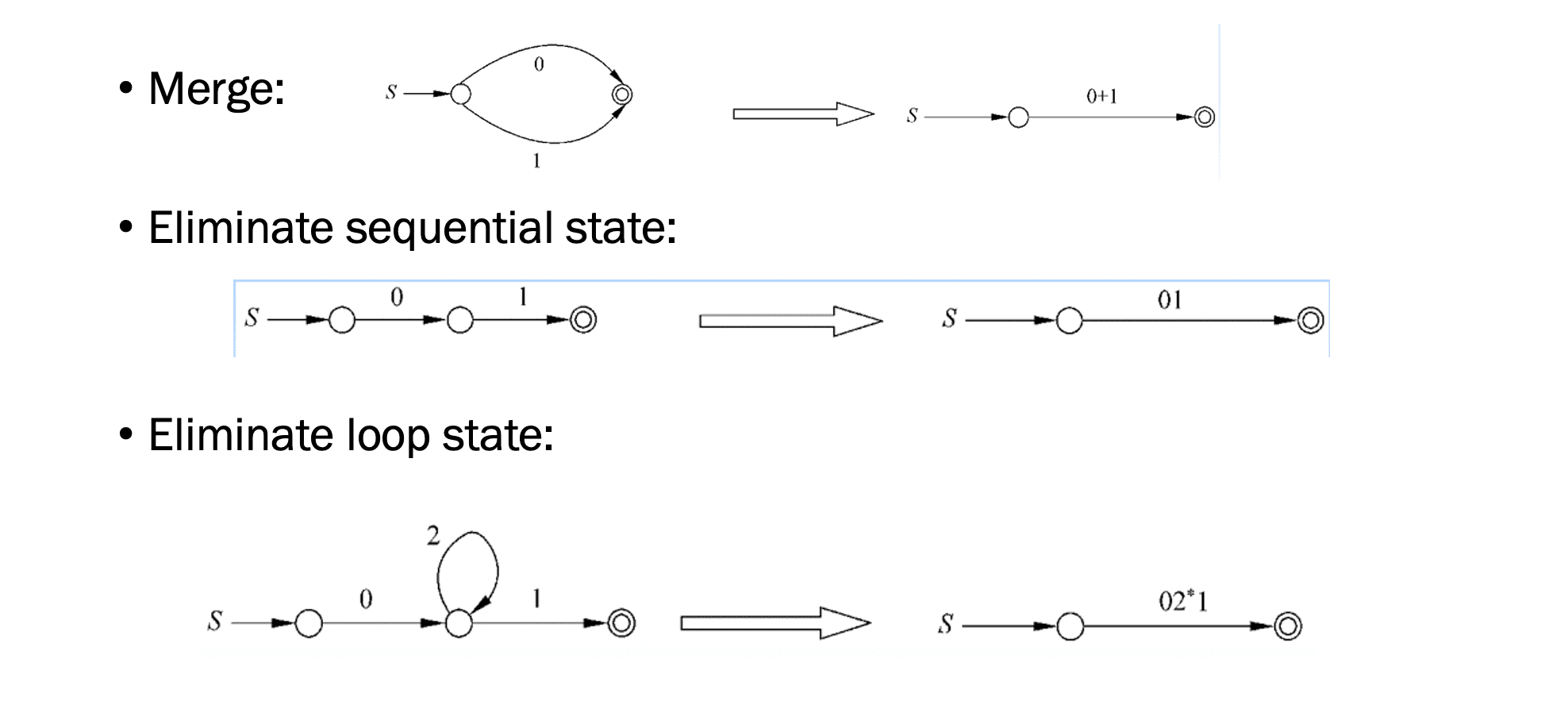
FA -> RE 的转换
RE -> FA
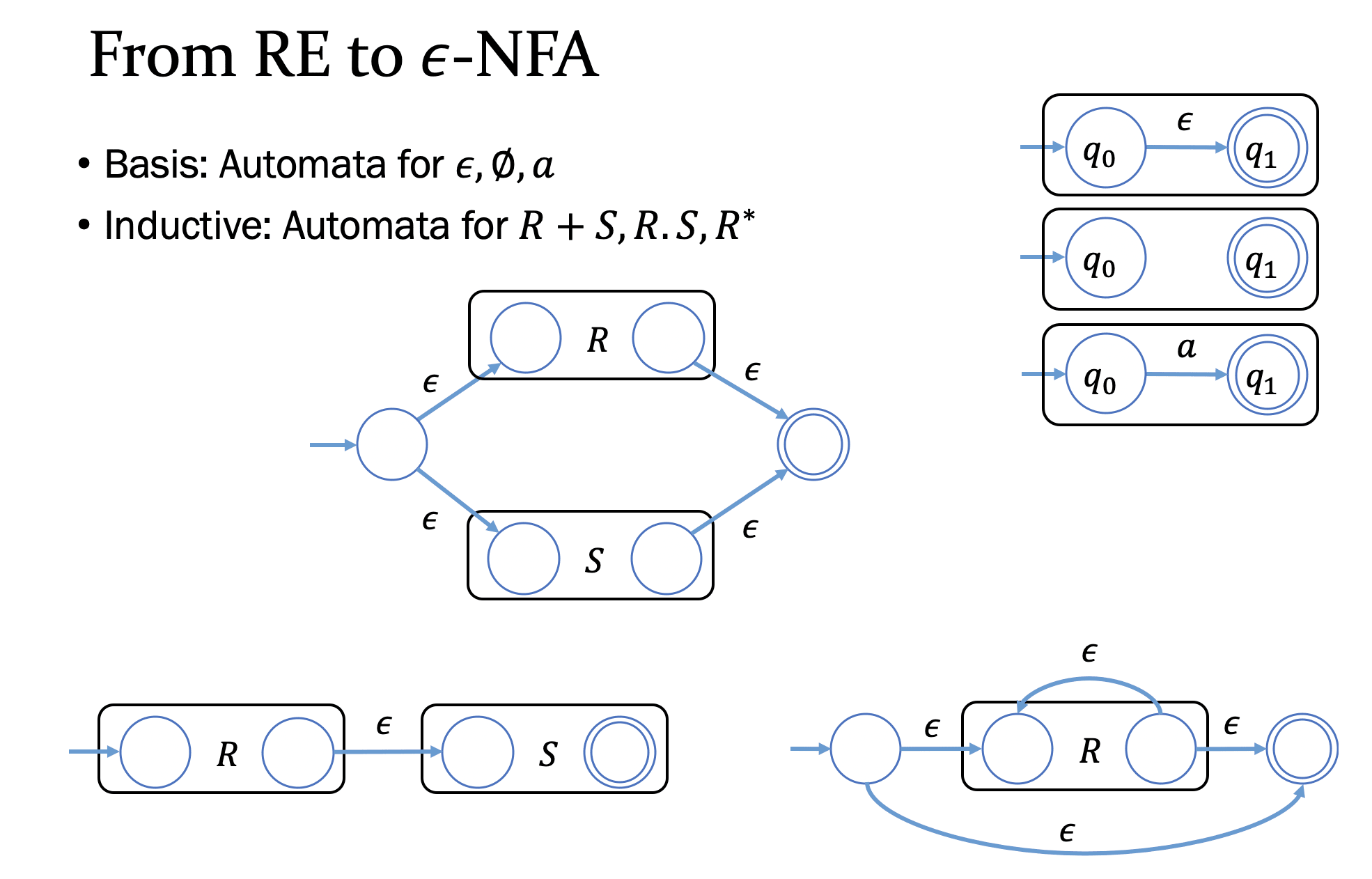
- Eg.
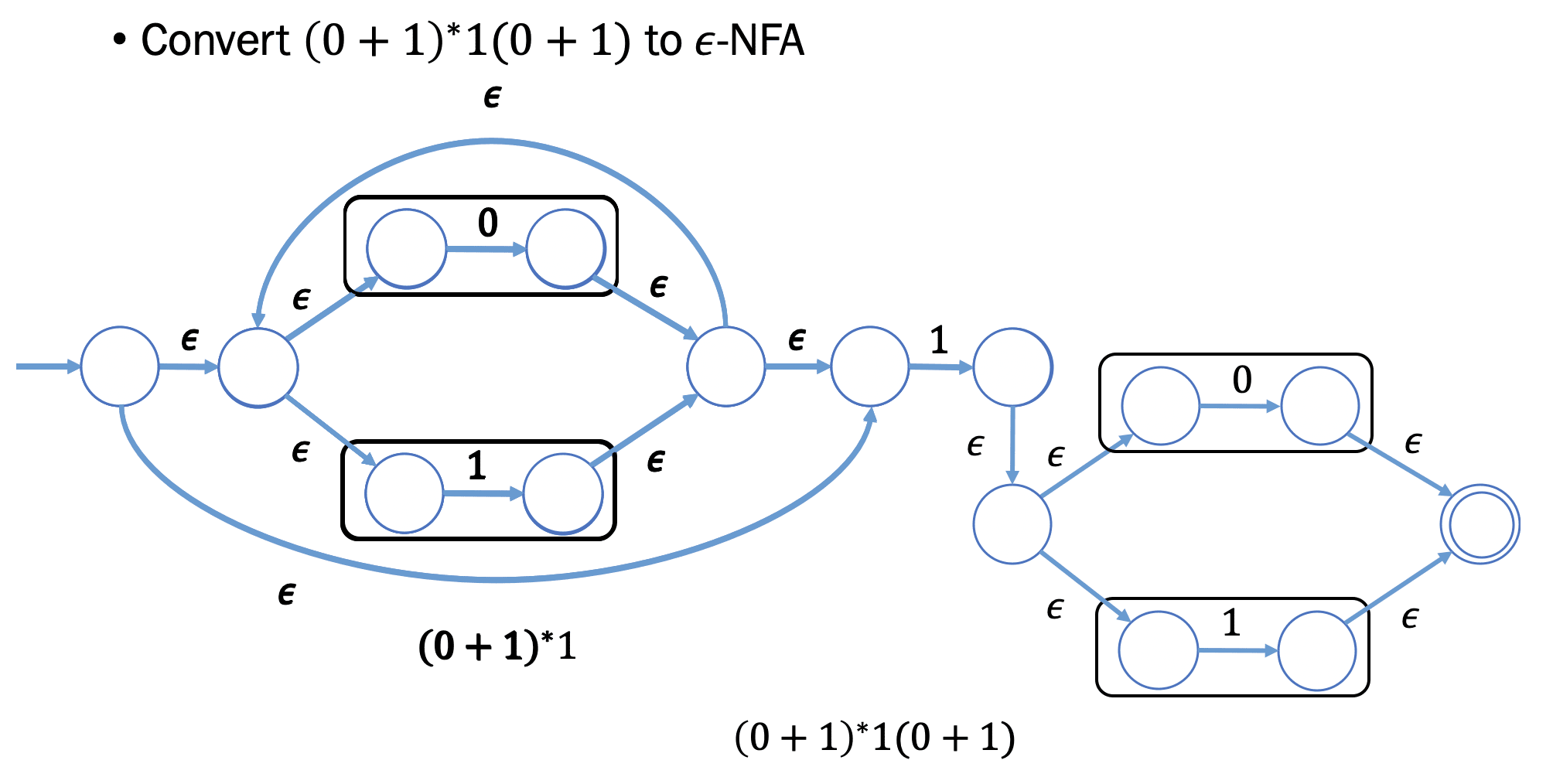
III: 上下文无关文法与下推自动机
上下文无关文法 CFG
Context Free Grammar CFG 需满足:,均有 成立(即左侧不可以含有终止字符,但右侧可以含多个 symbols,而不是正则语言中的右侧只允许一个)。
一些概念:
| E | T | F | P | id |
|---|---|---|---|---|
| Expression | Term | Factor | Primary | Identifier |
| 表达式 | 项 | 因子 | 初等量 | 标识符 |
上下文无关语言在并、乘积、闭包下是封闭的,在交、补运算下不封闭。 CFL 与 RL 的交是 CFL。
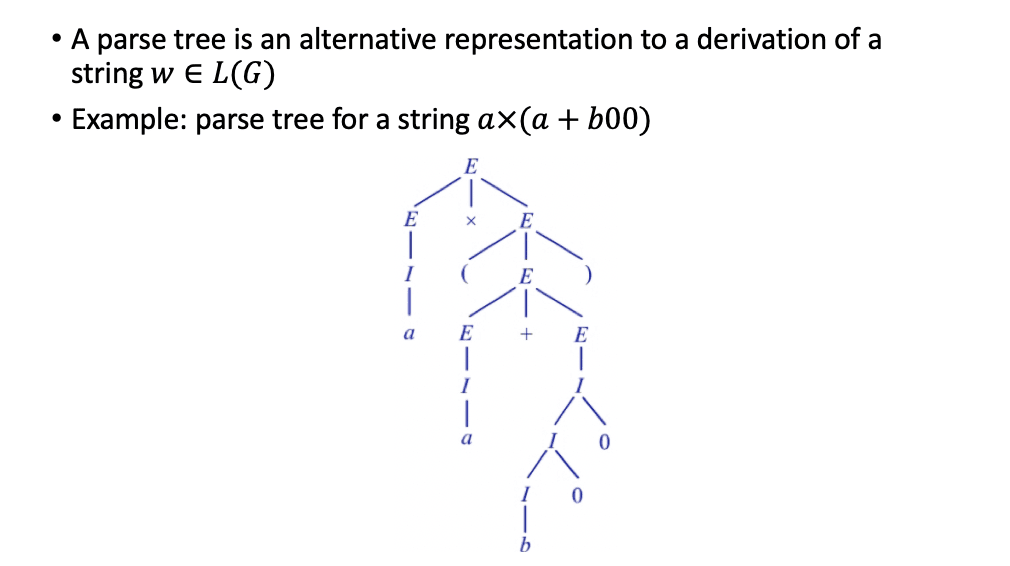
派生方式与二义性
-
极左派生 Leftmost Derivations ,在 派生过程中每一步都对最左变量进行替换(类似地有极右派生 Rightmost derivations),对应的规约有极左 / 右规约。
- 最右派生 aka 规范派生 Normal Derivation,规范派生产生的句型为规范句型 Normal Sentencial Form
-
二义性 Ambiguous Grammar:至少具两棵不同的派生树
-
== 判定 CFG 是否为 Ambiguous 是一个不可解问题==。
-
解决二义性的方法:增加优先级、增加标志等等
-
固有二义性 Inherent Ambiguity (并非所有语言都具备非二义性文法)
- 形如 的语言具备不同的派生树,具有固有的二义性,例如:
-

CFG 的化简
-
消除无用符号:
有用符号:X 有效,当存在转移
有用符号应当是可生成且可达的,非可达、非可生成的符号都需要被消去
- Generating: for some
- Reachable: for some
Eg.
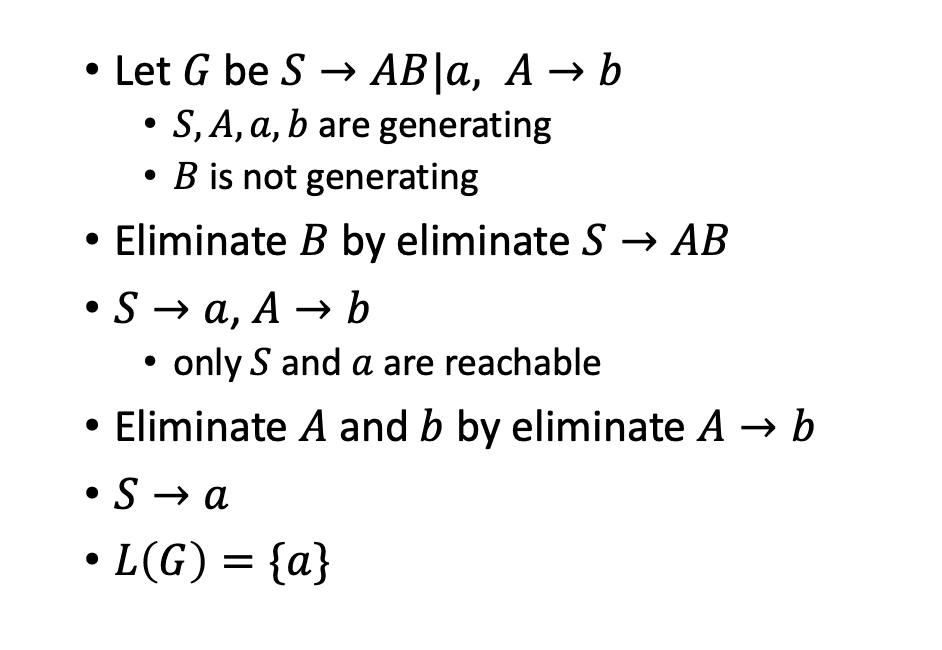
-
消除空转移
Nullable:A 是可空的当
计算 nullables:先令 ,递归向上规约得到所有
接下来做替换:若 A nullable,则 被替换成 ,最后消去所有
-
消除单位转移 Unit Production (形如 )
先令 ,如果 且 则将 (A, C) 添加至 G
接下来遍历 n (G),每一对 (A, B) 如果: 不是一个单位转移,则添加 添加至
范式
乔姆斯基范式 Chomsky Normal Form CNF
如果 CFG 中的所有产生式都有形式:
,,则为 CNF。
乔姆斯基范式中不允许存在 产生式、单一产生式,也不希望含有无用符号。
- CFL 转换为 CNF:处理所有推导结果长于 2 的,把 a 替换成新的 A,再增加
- 把所有长于 3 的级联分解成两个变量的转移,图示:
-
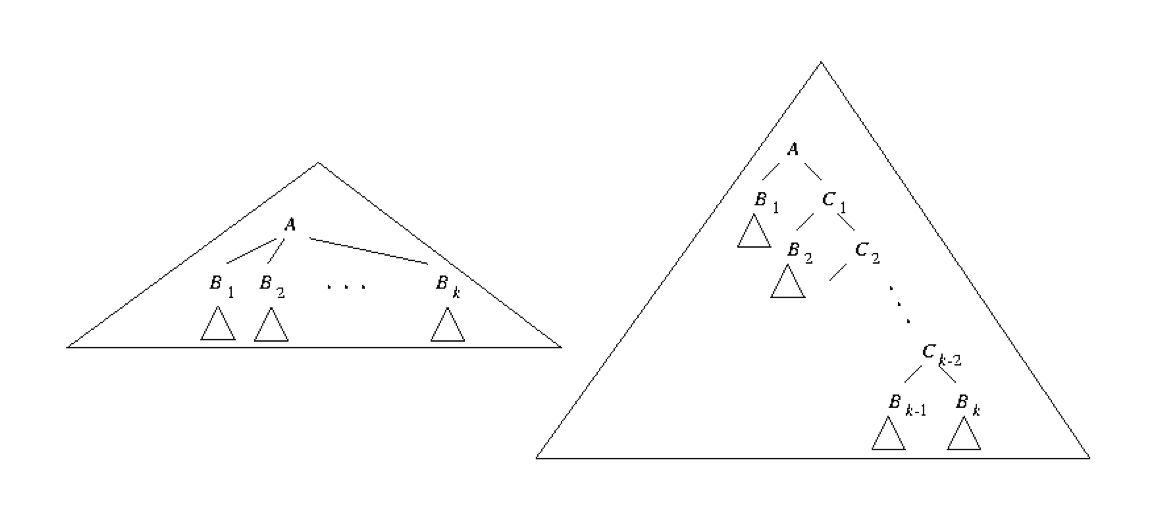
格雷巴赫范式 Greibach Normal Form GNF
如果 CFG 中的所有产生式都有形式 ,则为 GNF。
注意到右线性文法是一种特殊的 GNF。
CFL 的泵引理
类似正则语言的泵引理定义如下:
- 对于 CFL,存在一个 N 若 则改写 满足:
- 即有
例如,证明 不是 CFL:
下推自动机 Push Down Automaton PDA
PDA 与 CFG - 二型文法等价
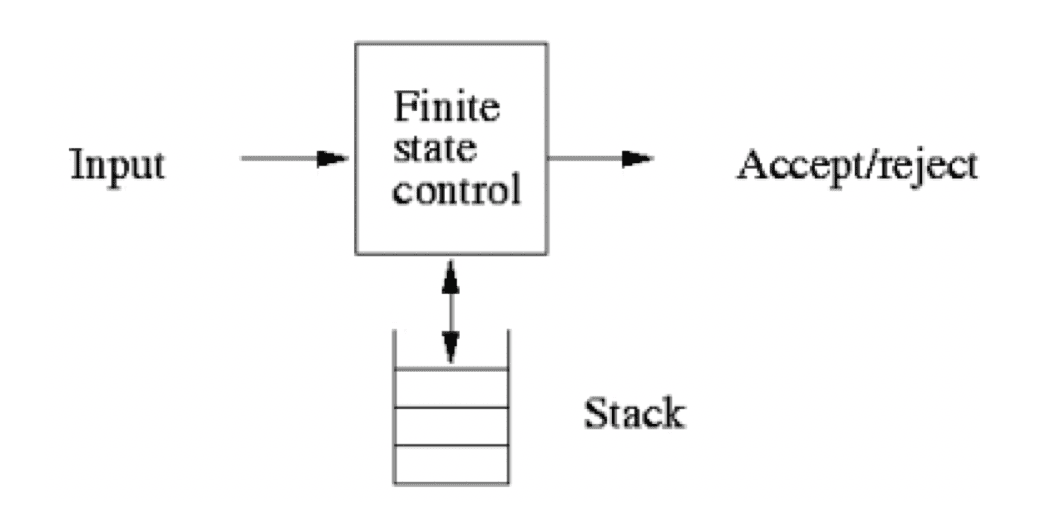
定义:一个七元组 :
-
Q 状态集合; 输入字母表; 栈符号表; 开始符号(栈底符号) 开始状态; 终止状态; 转移函数 ,形如: 为一次非空移动
- 形如: 为一次空移动,此情况下无论输入内容是什么,都可以选择直接将状态变为 。
-
一个例子:构造 ,其中 R 为倒序:
- PDA 在图形中表示如下,右侧表示栈 Z 在状态转移之前与之后的情况,栈顶位于左侧,栈底位于右侧: 表示空栈
-
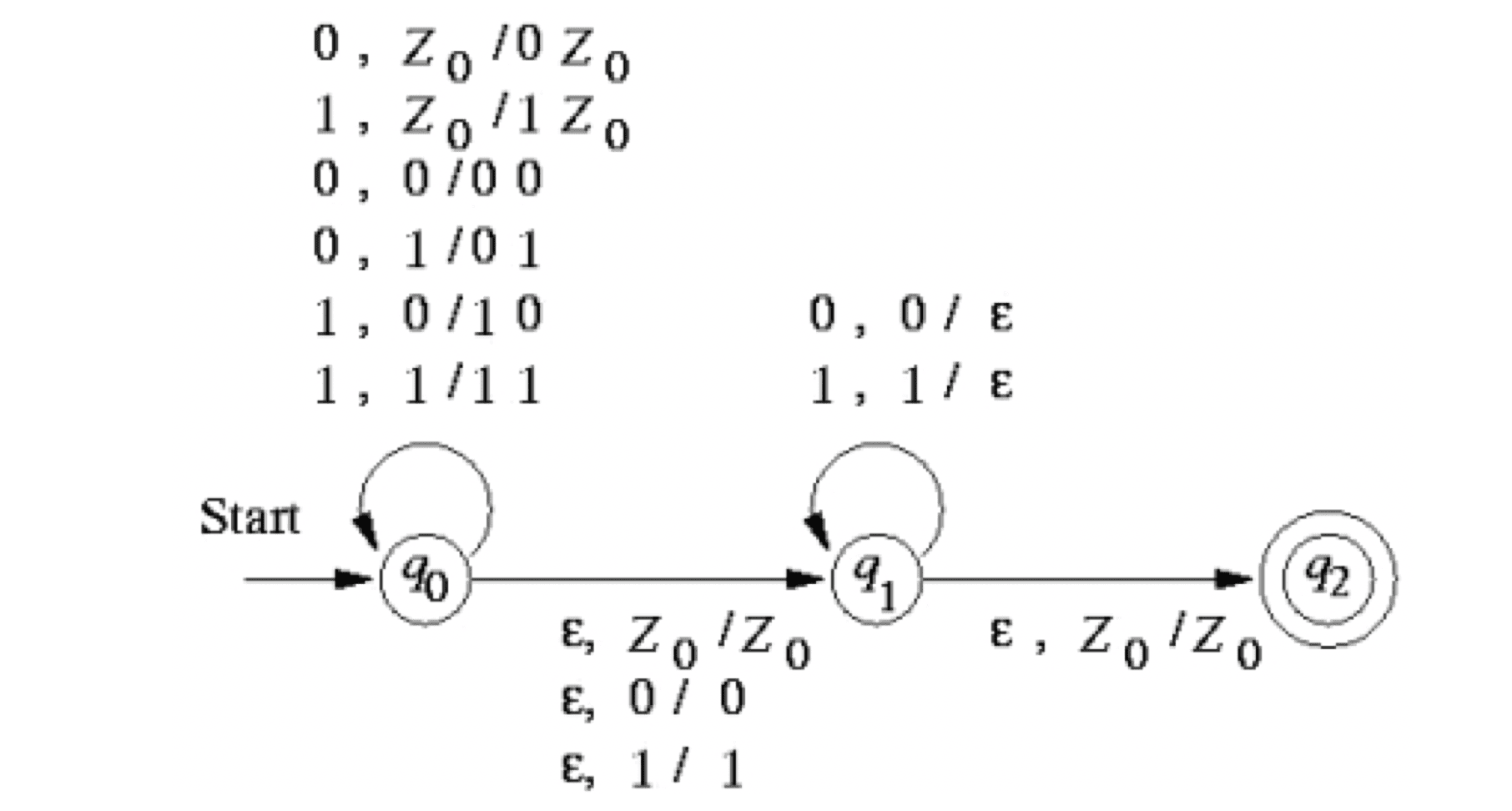
-
确定下推自动机 DPDA: 在 a 是 时总是空,且 非空则 非空。
- Regular language L(DPDA) Context-Free language
PDA 即时描述 Instantaneous Description
- 即时描述: 成为 M 的一个即时描述
- 一个非空移动的表示: ,其中 aw 为即将读入的字符串,M 之前位于状态 q,栈顶为 Z,进入状态 p 后 Z 被 替换。
- 同样有 的表达方式以表示特定次数的移动。
可使用 ID 描述上述 如下:()

PDA 接受的语言
- 以终止状态接受:
- 以空栈接受:
定理:两种接收方式是等价的。
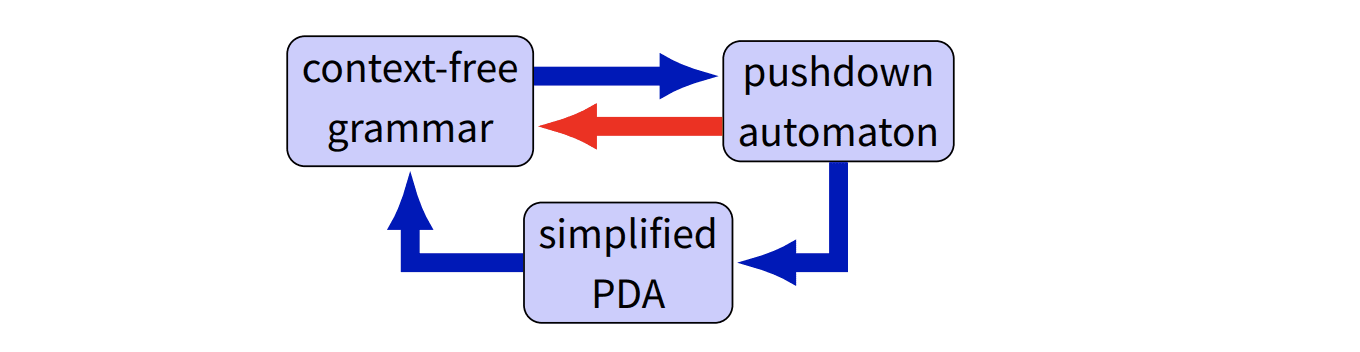
CFG 与 PDA 的等价性
L 是 CFG 当且仅当能被一个 PDA 接受。(两种接收方式)
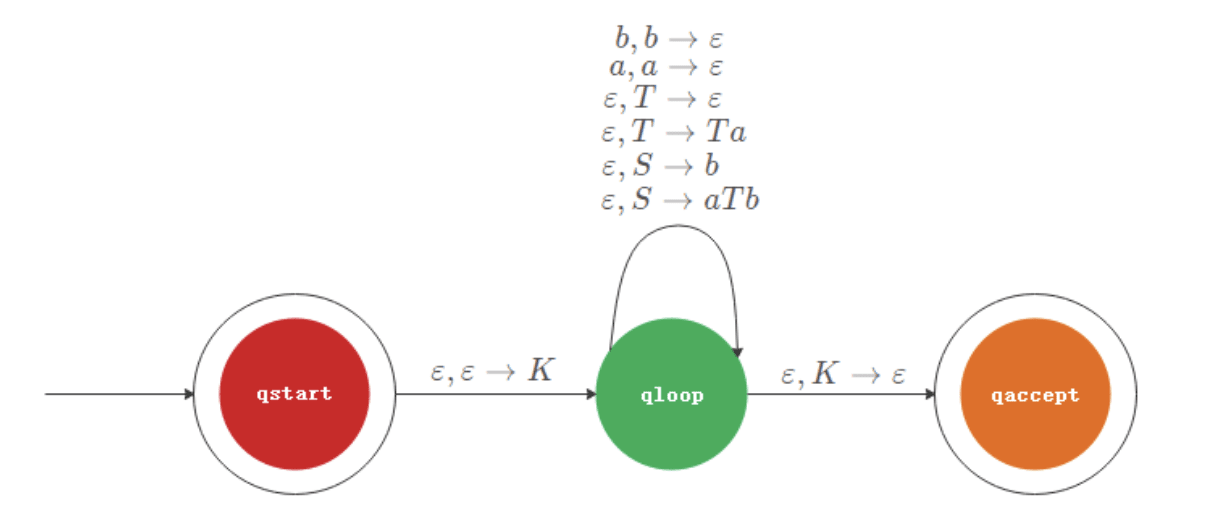
CFG -> PDA
模拟一个 CFG 的极左派生 :
-
对应一个 PDA 的操作,在栈 Z 中压入非终止字符,在栈上有终止字符时便弹出
-
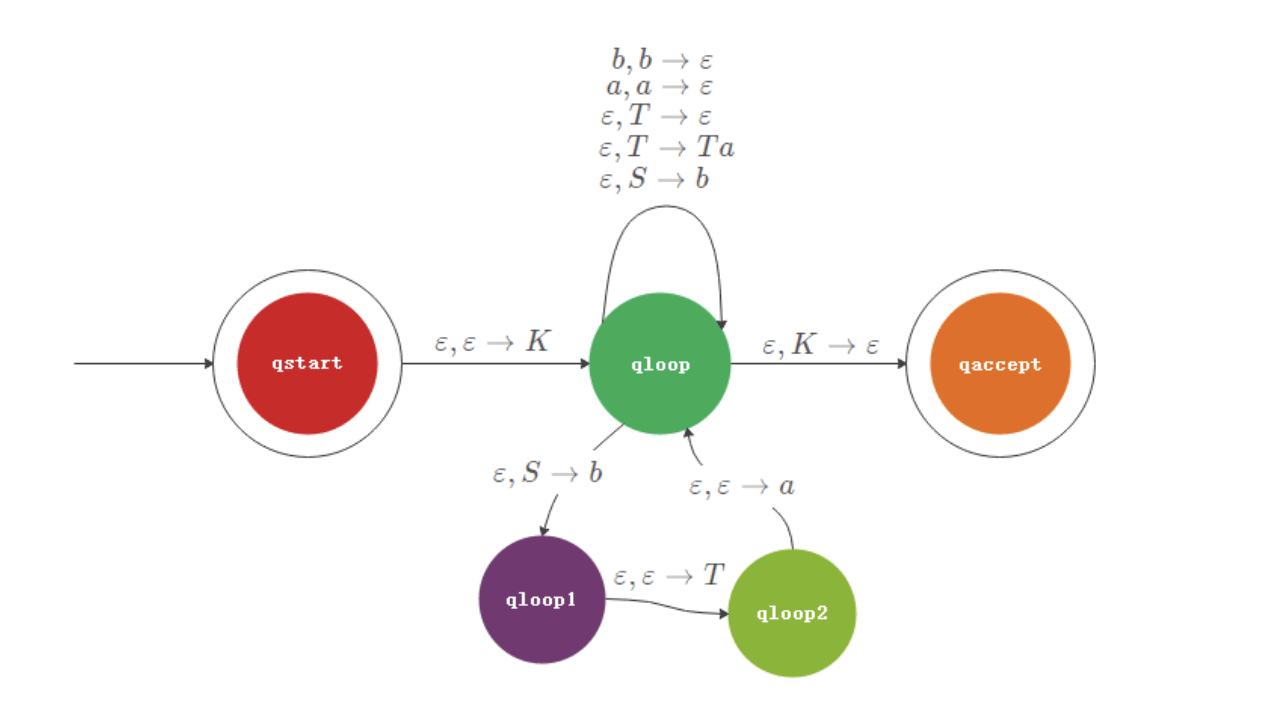
此时可能会有非法的指令(在栈中一字符(包括 只能由一个字符替换)),可以进行指令分解
分解 之后自动机如图所示:
以此类推进行指令分解。
PDA -> CFG
暂且省略。
IV: 图灵机与可计算型
图灵机 Turing Machine
TM:人们所接受的算法的形式化描述。与 TM 具有同样计算能力的还有 演算、递归函数、波斯特系统等。
定义:七元组 :
- Q 状态的有穷集合; 输入字母表; 带符号表(运行过程中的符号); M 的开始状态;F 终止状态;B 空白符(基本图灵机的概念); 转换函数,形如 ,表示在状态 q 读入符号 X,将状态更新为 p,并在 X 所在的方格中印刷符号 Y,接着向右 / 左移动一格。
如:
初始状态下,输入字符串依次放在条带上,指针注释第一个元素,状态为 。
TM 定义的语言为递归可枚举语言,即 0 型文法。
TM 即时描述 Instantaneous Description
TM 的即时描述为字符串 。
- q:目前状态;磁带指向第 i 个符号
- 其余符号表示最左侧的空白到最右侧的空白之间的所有字符
- 同样有 的表达方式以表示特定次数的移动
TM 作为非负整函数的计算模型
对非负整数编码后图灵机具有计算能力。
例如计算 n+m 的图灵机可以将字符串编码为 ,利用图灵机扫描,修改 1 的位置即可。
构造方式
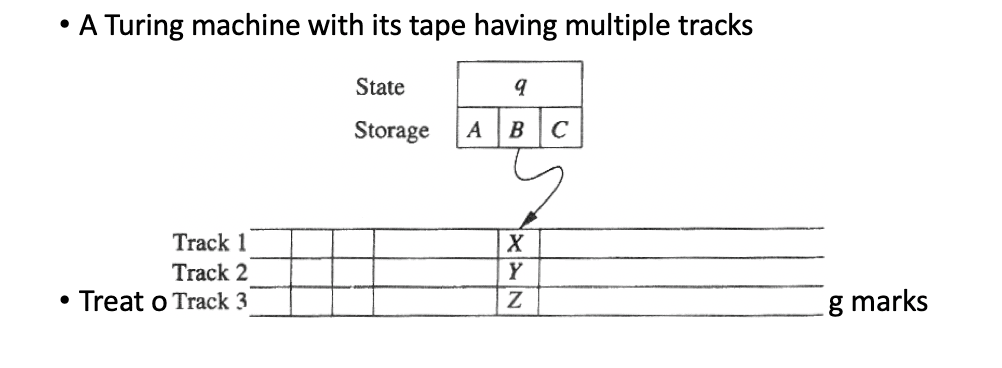
Multiple Tracks 多轨
计算能力和单轨相同,可以将存储的值复合为 {X,Y,Z} 即变成单带。
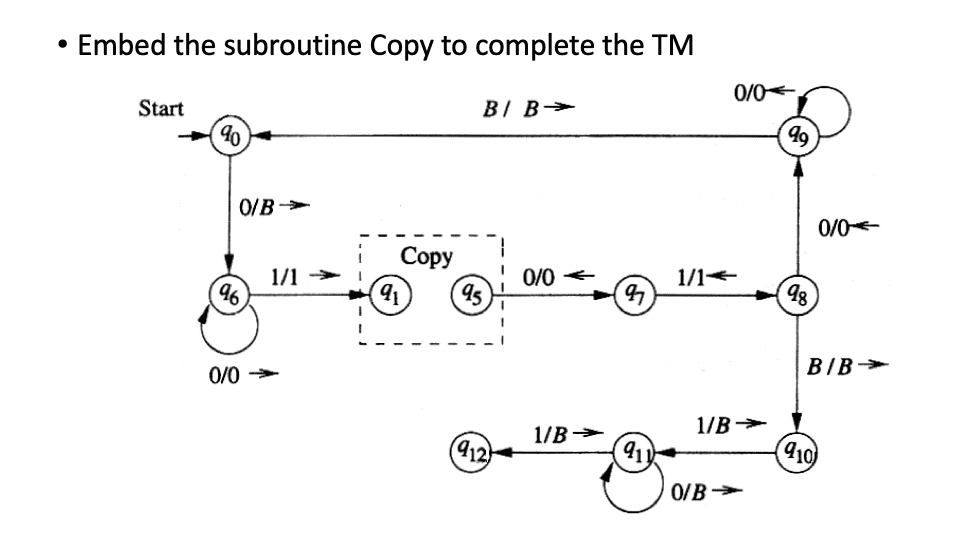
Subroutine 子图
TM 拓展及变型
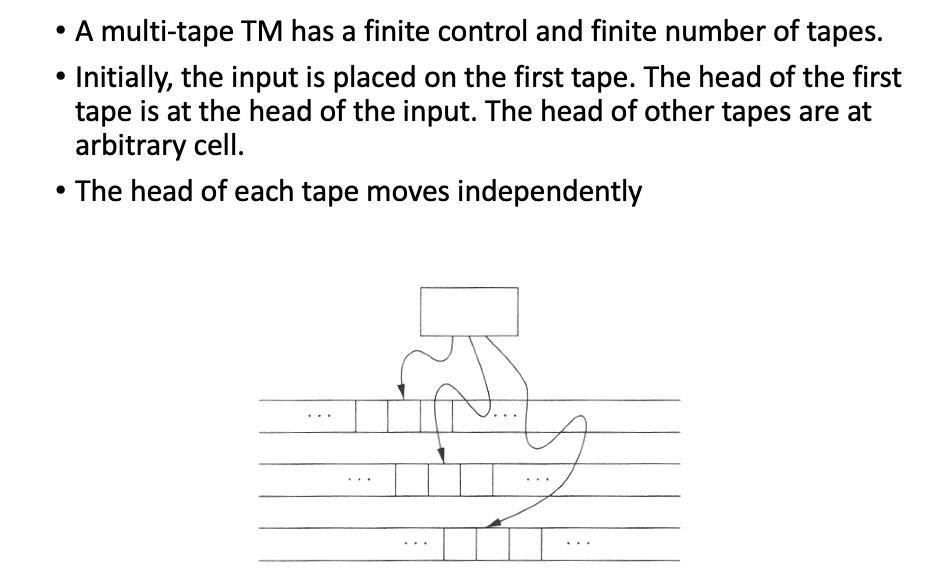
Multi-tape Turing machine 多带处理器
本质上也和基本图灵机等价。
Non-deterministic TM 非确定图灵机
对于每一个转移函数 ,非确定图灵机具有一系列转移结果
只要有一条路径到达最终状态即可接收。
可计算性 Computability
(仅作了解)
可计算型的问题:对于问题给出是与否的判定。
- 如果一个问题的语言是递归的,则可判定 Decidable
- 如果一个问题的语言不可递归,则不可判定 Undecidable
Example:
上述程序查找 的 x, y, z 整数元组,查找到则输出 hello, world。该问题 Undecidable。
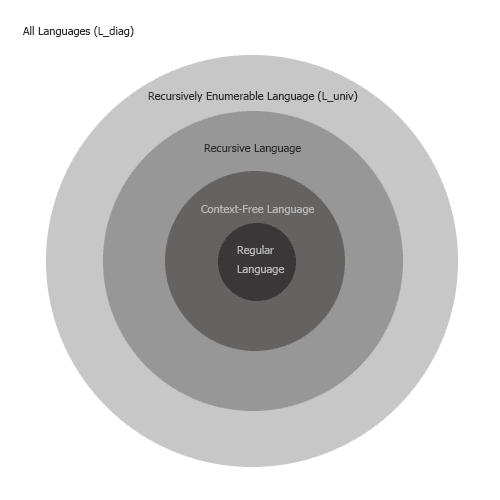
- Non-RE language 非递归可枚举语言(一个不能递归枚举字符串中的所有语言)
- 递归可枚举语言:可以用类似穷举的算法在有限时间内判定一个元素属于该集合
- 停机问题 Halting Problem: 不存在一个算法,能够判断任意图灵机
在任意字符串
上否停机。
- 图灵机编码:
NP 与 P
- P 问题:可以在多项式时间内求解的判定问题 Polynomial Problem
- NP 问题:Non-Polynomial 不可以在多项式时间内解决的问题
- NPC 问题:Non-Polynomial Complete NP 中的某些问题的复杂性与整个类的复杂性相关联。这些问题中任何一个如果存在多项式时间的算法,那么所有 NP 问题都是多项式时间可解的。这些问题被称为 NP - 完全问题 (NPC 问题)。
The End