关于函数依赖，正则覆盖与 BCNF 范式分解

复习数据库系统时刚好接触到这部分内容。有几个相对重要而难理解的概念，教材的语言十分形式化，在这里稍作一下直观的整理。

函数依赖 Functional Depencendy

可以理解为属性 R 中的一个元组 t1 （这个元组需要是这个关系的 super key，即能够标识整个属性集合）决定了另一系列元组 t2 的值。例如部门决定了预算，则有函数依赖 $dept \rightarrow budget$ 。

函数依赖分为平凡函数依赖和非平凡函数依赖。函数依赖 $X \rightarrow Y$ 中，若 Y 为 X 的子集，则为平凡函数依赖。直观的字面理解就是这种依赖非常的 “普通”，在所有关系中都满足。例如任何属性都能决定自身，函数依赖 $A \rightarrow A$ 恒成立。若 Y 不为 X 的子集，则为非平凡函数依赖。通常我们讨论的是非平凡函数依赖。

完全函数依赖指的是 $X \rightarrow Y$ 中，X 已经包含了最少的属性。再减少任何一个属性都会破坏函数依赖。例如预算可以完全依赖于部门和年份，这就是一个完全依赖。

而部分函数依赖指的是在 $X \rightarrow Y$ 仍然存在 X 的子集 X' 满足 $X' \rightarrow Y$ ，例如 $dept\_id, dept\_name \rightarrow budget$ 中，左侧仅依赖 dept_id 就可以决定预算的值，那么这就是一个部分函数依赖，预算部分依赖于部门 ID 和部门名字。

还有一个传递函数依赖的概念，如果 $X \rightarrow Y$ ， $Y \rightarrow Z$ ，则 $X \rightarrow Z$ 成立。这就是一个传递函数依赖。如员工 -> 部门 ID，部门 ID -> 预算，那么员工 -> 部门预算就是一个传递函数依赖。

通常使用 F 来表示关系 R 中的所有函数依赖，F⁺ 来表示由 F 推断出的所有依赖（运用 Armstrong 定理）。

Boyce-Codd 范式 BCNF

BCNF 消除了所有基于函数依赖能够发现的冗余，在 BCNF 范式中，对与所有函数依赖 $X \rightarrow Y$ ，要么 X 是 R 的一个 super key，如果不是的话那么这个依赖必须是平凡依赖。

教材中不是 BCNF 的一个例子:

inst_dept (ID, name, salary, dept_name, building, budget)

这里存在非平凡函数依赖 dept_name -> budget。但是 dept_name 显然不是这个关系的一个 super key，因为光从部门名称不能标识一个教师的所有信息。这于是就违背了 BCNF 的条件。直观来讲，满足 BCNF 的关系中的所有这种依赖关系，都应当是由 super key 来推断出来的，除了 super key 的推断关系以外，不能再有其他的推断关系。

其实在设计数据库的时候 BCNF 的使用非常直观。简化地例子是，有两个实体学生和学院，在设计数据库的时候我们会很直观地把学生及其信息放在一个表中，学院及其信息放在另一个表中，再用一个学生表中的属性来关联学生和部门的关系，而不会在一个表中放下学生及其学院及其学院的信息。这种很直观的冗余就违背了 BCNF。

那么 BNCF 的分解也可以直观来理解。如果存在一冗余的非平凡依赖，把这个依赖单独提取出来成为一个新的关系即可。

属性闭包 Attribute Closure 与正则覆盖 Cononical Coverage

首先有一个属性闭包的概念。由一个属性能够推断出来的所有函数依赖的属性集合为属性的闭包，记作为 $\alpha ^{+}$ 。

属性闭包除了可以测试 super key （检查 $\alpha ^{+}$ 是否包含了所有属性）和判断函数依赖（检查 $\beta$ 是否属于 $\alpha ^{+}$ ）以外，还可以用来方便地计算 F⁺。对于每一个属性 x 计算闭包 S，然后依次输出 x -> S。

接下来有无关（extraneous）属性的概念。如果去除函数依赖中的一个属性，不改变该函数依赖集的闭包，则称该属性是无关的。计算方式可以直观理解为：如果有一个函数依赖 $\alpha \rightarrow \beta$ ，且 $A \in \beta$ ，那么测试 A 是否是无关属性的方法就是从 F 中去掉 $\alpha \rightarrow \beta$ 这一依赖，增加 $\alpha \rightarrow (\beta - A)$ 这一依赖，检查能不能从 $\alpha^{+}$ 中推出 A，如果仍然能够推出，那么 A 就是多余的。

正则覆盖可以理解为是消去了无关元素的函数依赖集。计算方法是从 F 使用合并的方式来替换掉所有的依赖，接下来依次删除所有的无关元素。

一个例子：

BCNF 的分解

首先这里由引入了无损连接的概念。即分解后的关系和之前未分解的关系模型相比没有信息损失。形式化的表达为：

\Pi_{R_1}(r) \bowtie \Pi_{R_2} (r) = r

一个有损分解的例子是，将员工分解为

employee1(ID, name)
employee2(name, street, city, salary)

在 Natural Join 之后由于可能有重名存在，这个分解便是有损的。

分解 BCNF 的步骤可以简化为以下几步：

寻找 R 中一些属性 $\alpha$ 的的闭包，如果这个属性的闭包没有包含 R 中的所有元素（即不为 super key），且不为平凡函数依赖，那么需要拆解。
拆解方法：若这个非平凡依赖为 $\alpha \rightarrow \beta$ ，则将原来的 R 变为 $R - \beta$ ，并构造一个新的关系 $\alpha \cup \beta$ 。
依次拆解，直到全部拆解完毕。

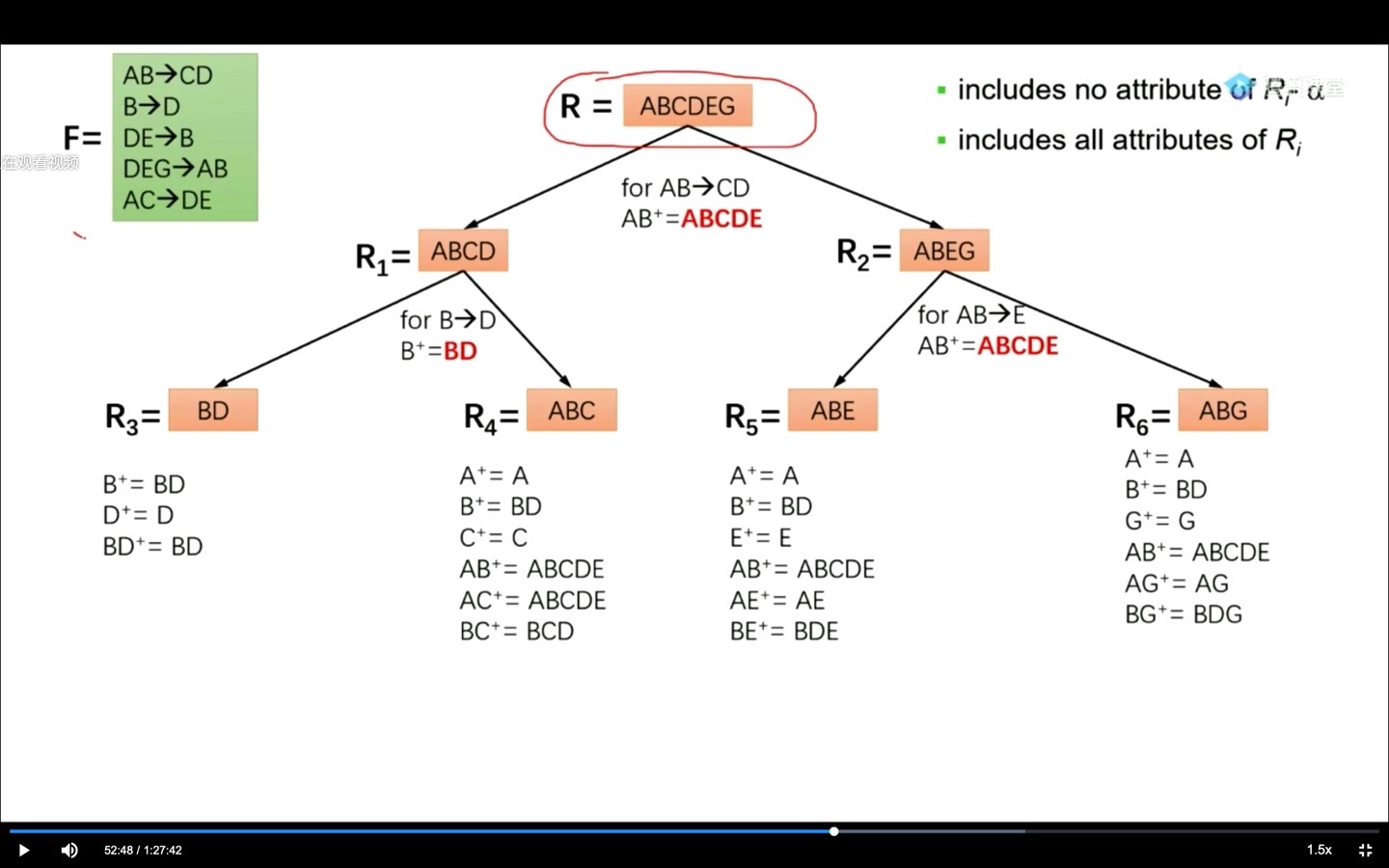
图解展示这个过程如下：

在这个例子中，为了从 R₂ 得到 R₅，中途的 AB -> E 可通过函数依赖的传递和拆解得到：

已知 AB -> CD, AC -> DE
则 AB-> ACD, ACD-> DE
则 AB -> DE
则 AB -> E

如此即可得到这一关系的 BCNF 拆解，且满足无损连接，因为有 $R3 \bowtie R4 \bowtie R5 \bowtie R6 = R$ 。

关于函数依赖，正则覆盖与 BCNF 范式分解

目录

函数依赖 Functional Depencendy

Boyce-Codd 范式 BCNF

属性闭包 Attribute Closure 与正则覆盖 Cononical Coverage

BCNF 的分解